Hello LUYEE

| algorithm leetcode array backtracking |

主要收获 - 1

规范了 回溯算法 的经典写法。这是一个非常常用的算法。需要肌肉记忆。

主要收获 - 2

复习和强化了 排序以后，不重复遍历 的思想。

主要收获 - 3

一个普遍常识是，官方容器List的效率和Array差不太多。这次特意实际做了比较。证实了这种说法。

题目

Given a set of candidate numbers (C) (without duplicates) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.

The same repeated number may be chosen from C unlimited number of times.

Note: All numbers (including target) will be positive integers. The solution set must not contain duplicate combinations. For example, given candidate set [2, 3, 6, 7] and target 7, A solution set is:

[
  [7],
  [2, 2, 3]
]

暴力递归回溯 \(O(n^n)\)

[8,7,4,3]，目标值11。先排序，得到[3,4,7,8]。对数组中的每个数，只要加上历史小于目标值就开下一层递归。

初始累积总和 = 0，

0+3 < 11    >>>    [3], 递归面对[3,4,7,8]
0+4 < 11    >>>    [4], 递归面对[3,4,7,8]
0+7 < 11    >>>    [7], 递归面对[3,4,7,8]
0+8 < 11    >>>    [8], 递归面对[3,4,7,8]

注意！ 这里虽然先排序了，但并没有利用到排序的所有好处。排序仅仅是用来做剪枝。当找到[4,7]是正确解之后，就不再遍历[4,8]的组合，因为肯定会溢出。但其实排序能带来更大好处。

代码

public class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        List<List<Integer>> result = new ArrayList<>();
        recursion(new ArrayList<Integer>(), 0, candidates, target, result);
        return result;
    }
    public void recursion(List<Integer> register, int sum, int[] candidates, int target, List<List<Integer>> result) {
        for (int i : candidates) {
            if (sum + i > target) { break; } // 剪枝
            List<Integer> copy = new ArrayList<>(register);
            copy.add(i);
            if (sum + i == target) {
                Collections.sort(copy);
                if (! result.contains(copy)) {
                    result.add(copy);
                }
            } else {
                recursion(copy,sum+i,candidates,target,result);
            }
        }
    }
}

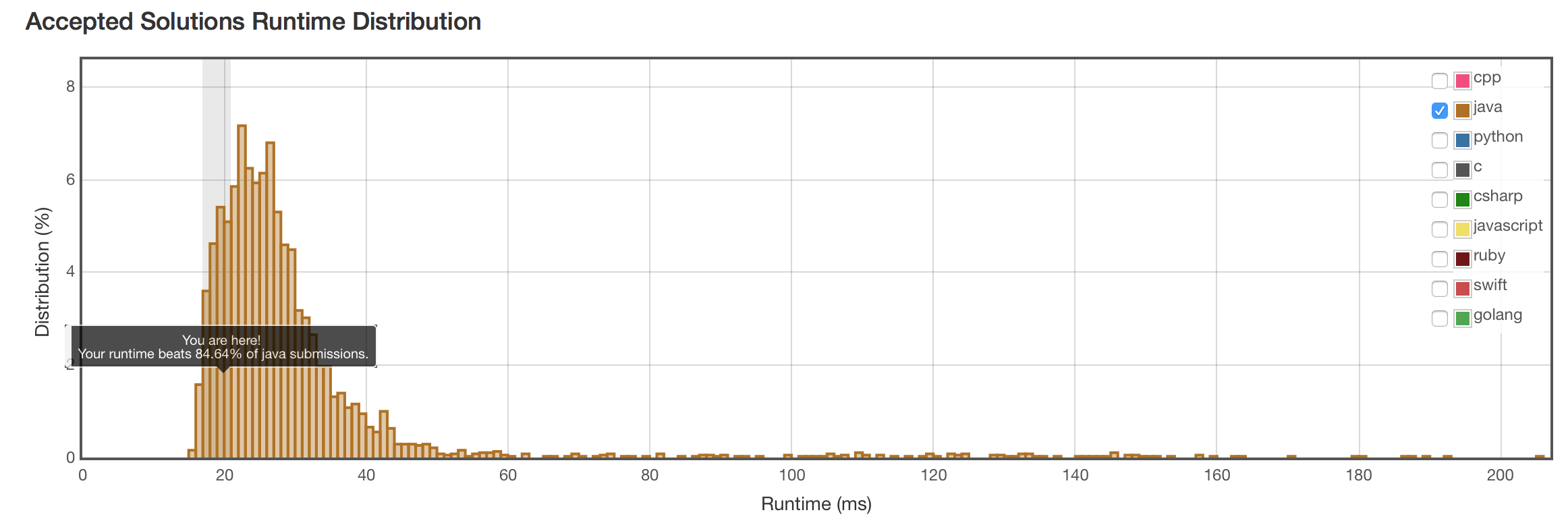
结果

So stupid, but it works. combination-sum-1

顺序遍历，不重复 \(O(2^n)\)

因为[8,7,4,3]排序后得到[3,4,7,8]。对于可能的三个结果：[3, 4, 4], [3, 8], [4, 7]。只要遍历的时候加一个指针，坚持不回退取更小的数，就不会得到重复结果。

举例来说，考虑[4,7]。因为第一个数取了4。就不需要再回头取3，得到[4,3,3]和之前的[3,4,4]重复。所以第一个数取了[4]以后，只需要考虑>= 4的数即可。

总的来说，对于[3,4,7,8]，我们遍历的顺序如下，

[3]，从3开始，肯定有3，可能有4,7,8的所有组合。
[4]，从4开始，没有3，肯定有4，可能有7,8的所有组合。
[7]，从7开始，没有3，4，肯定有7，可能有8的所有组合。
[8]，从8开始，没有3，4，7，只有8的所有组合。

这样一来，减少了迭代的数量，复杂度一下子从全排列的\(O(n^n)\)降到全组合的\(O(2^n)\)。而且得到的结果也不需要去重，当然也不需要去重前的排序。

这是非常典型的循序遍历的例子！

代码

public class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        List<List<Integer>> result = new ArrayList<>();
        recursion(new ArrayList<Integer>(), 0, candidates, 0, target, result);
        return result;
    }
    public void recursion(List<Integer> register, int sum, int[] candidates, int start, int target, List<List<Integer>> result) {
        for (int i = start; i < candidates.length; i++) {
            int newSum = sum + candidates[i];
            if (newSum > target) { break; }
            List<Integer> copy = new ArrayList<>(register);
            copy.add(candidates[i]);
            if (newSum == target) {
                result.add(copy);
            } else {
                recursion(copy,newSum,candidates,i,target,result);
            }
        }
    }
}

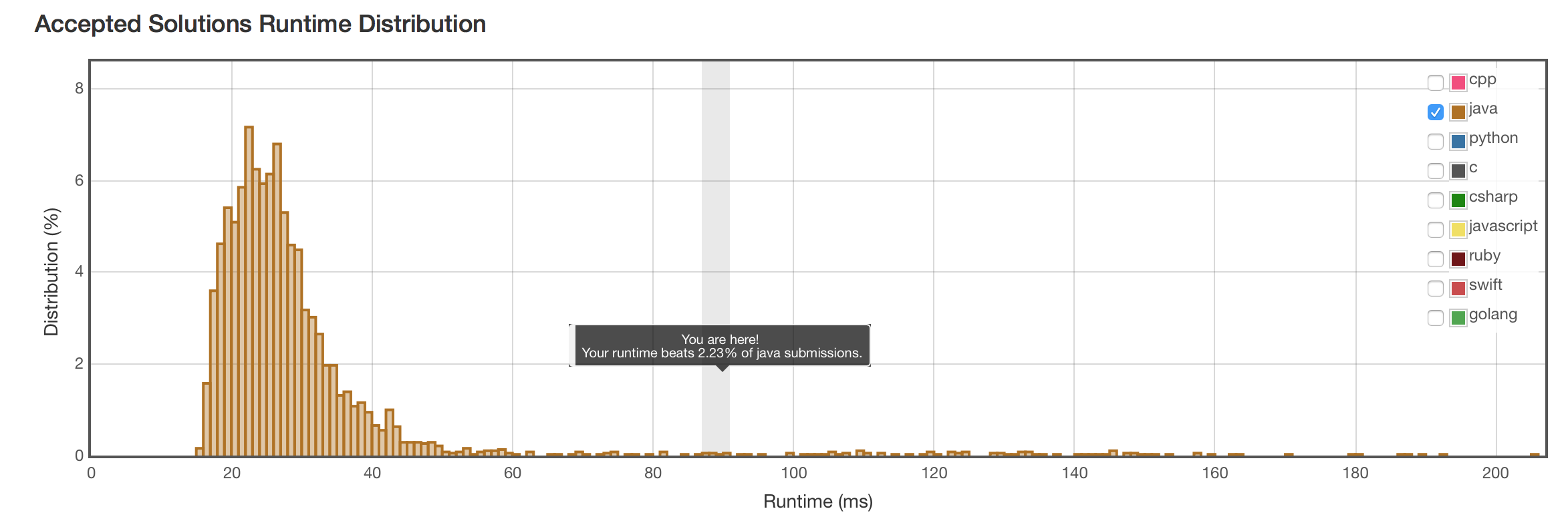
结果

银弹！ combination-sum-2

尝试用`Integer[]`替代`ArrayList<Integer>`提高效率，失败！

结果证明，老老实实用Collection Framework的容器，效率不必折腾Array低。

代码

public class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        List<List<Integer>> result = new ArrayList<>();
        recursion(new Integer[0], 0, candidates, 0, target, result);
        return result;
    }
    public void recursion(Integer[] register, int sum, int[] candidates, int start, int target, List<List<Integer>> result) {
        for (int i = start; i < candidates.length; i++) {
            int newSum = sum + candidates[i];
            if (newSum > target) { break; }
            Integer[] copy = Arrays.copyOf(register,register.length+1);
            copy[copy.length-1] = candidates[i];
            if (newSum == target) {
                result.add(new ArrayList<Integer>(Arrays.asList(copy)));
            } else {
                recursion(copy,newSum,candidates,i,target,result);
            }
        }
    }
}

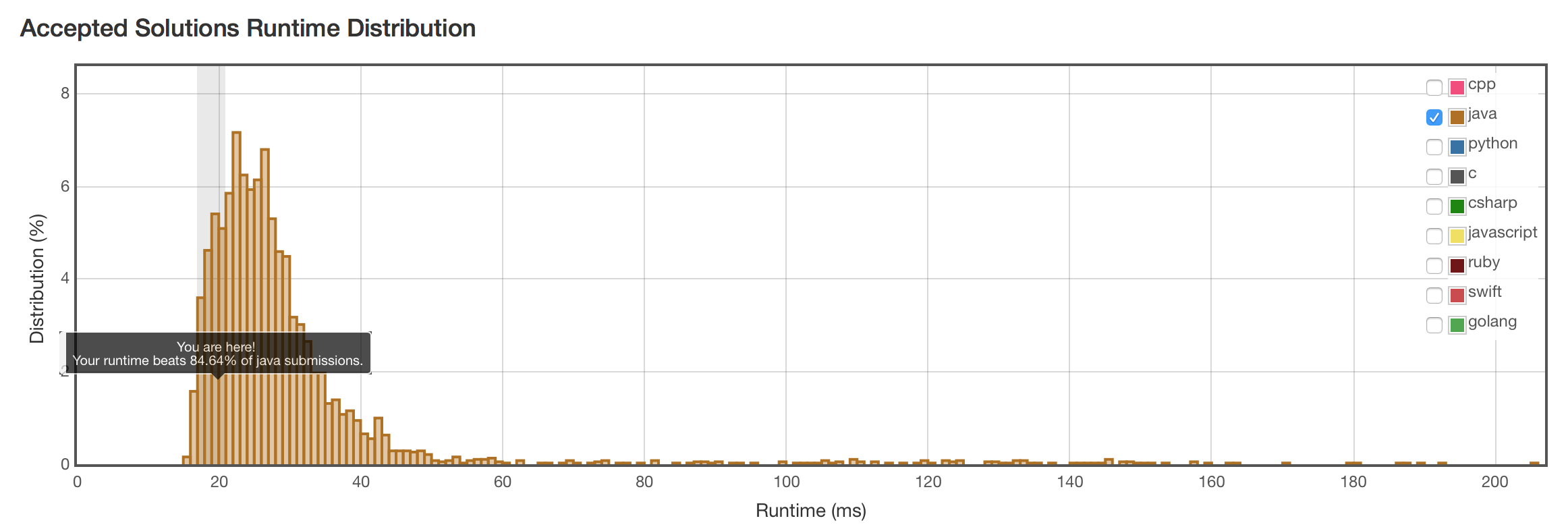
结果

反而比老老实实用ArrayList慢。 combination-sum-3

重点来啦：标准的回溯算法 \(O(2^n)\)

虽然上面的写法都对。思想也是标准的回溯算法。但有个缺点，每次传递累加列表的时候，都不敢直接在当前列表上插入元素。都是拷贝一个新数组。这样需要空间资源增多。执行过程中会产生很多中间列表对象。

List<Integer> copy = new ArrayList<>(register);
copy.add(candidates[i]);

而且这样的写法也没有体现真正 回溯算法 的精髓，就是回溯。之所以叫回溯，就是说不管对不对，先往这条路走，不对再退回来。

重点细节，看下面代码中的注释。

代码

public class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        List<List<Integer>> result = new ArrayList<>();
        backtrack(new ArrayList<Integer>(), target, candidates, 0, result);
        return result;
    }
    public void backtrack(List<Integer> temp, int remain, int[] candidates, int start, List<List<Integer>> result) {
        if (remain == 0) {
            result.add(new ArrayList<Integer>(temp));
            return;
        }
        for (int i = start; i < candidates.length; i++) {
            if (remain < candidates[i]) { break; } // 剪枝。当发现某个数太大，后面的更大的数也不用尝试了。
            // 回溯算法的精髓就体现在这三行上
            temp.add(candidates[i]); // 先插入新元素，递归下去。
            backtrack(temp,remain-candidates[i],candidates,i,result);
            temp.remove(temp.size()-1); // 递归结束，再删掉元素，继续迭代。
        }
    }
}

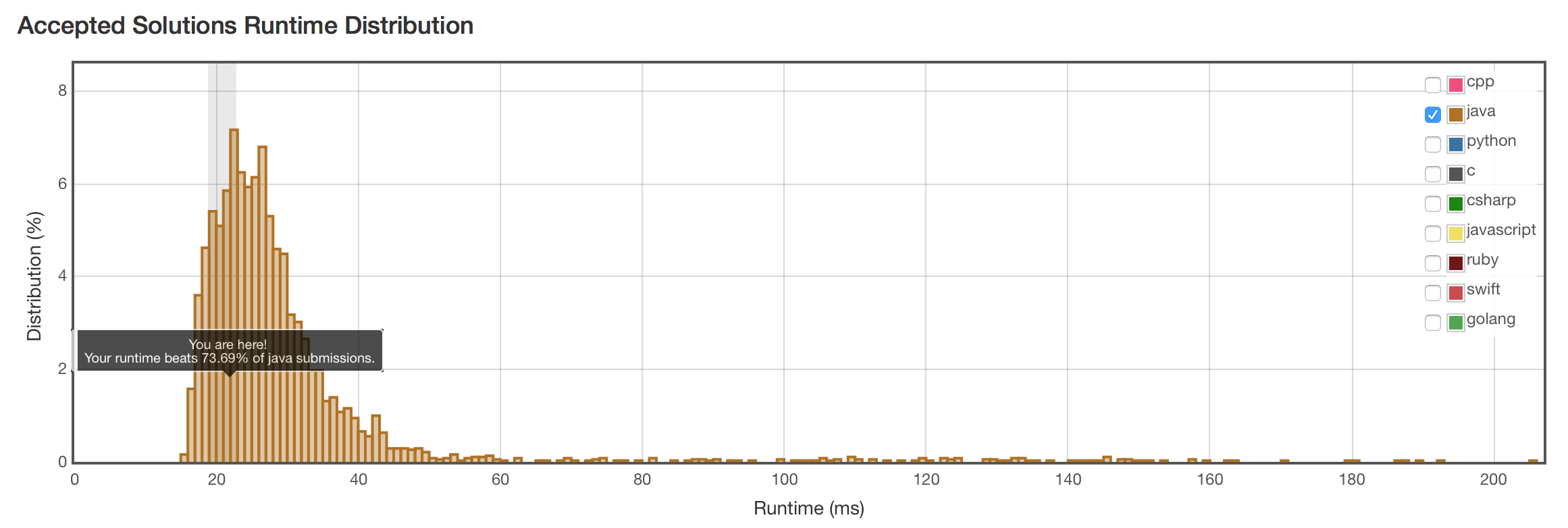
结果

combination-sum-4

Leetcode - Algorithm - Combination Sum